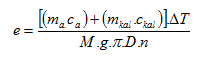Tara Mekanik Panas

TEORI DASAR

Kalor  merupakan energi yang ditransfer dari satu benda kebenda lain karena adanya perbedaan suhu. Sedangkan panas merupakan sebuah sifat, panas merupakan akibat dari energi kalor tersebut yang dapat kita rasakan.

Kalor dapat berpindah dari satu tempat ke tempat lainnya dengan tiga cara, yaitu :

1. Konduksi

Merupakan proses perpindahan kalor tanpa disertai perpindahan partikel. Pada konduksi, energi tersebut ditransfer dari molekul atau elektron dengan energi kinetik yang lebih tinggi ke yang mempunyai energi kinetik yang lebih rendah ketika mereka bertumbukan. Konduksi non logam adalah perpindahan dari satu partikel yang sedang bergetar ke partikel lainnya melalui tumbukan. Sedangkan konduksi logam adalah perpindahan kalor melalui elektron-elektron bebas.

Berdasarkan kemampuan menghantar kalor, zat dibagi atas dua golongan besar, yaitu konduktor dan isolator. Konduktor adalah zat yang mudah menghantarkan kalor. Contohnya adalah logam, karena elektron-elektron bergerak bebas sehingga merupakan konduktor yang baik. Sedangkan isolator adalah zat yang sukar menghantarkan kalor. Contohnya adalah kayu.

2. Konveksi

Merupakan perpindahan kalor yang dilakukan oleh pergerakan fluida akibat perbedaan massa jenis atau transfer energi dengan cara perpindahan massa menempuh jarak yang cukup jauh. Contoh konveksi dalam keseharian adalah arus konveksi udara yang membawa asap bergerak ke atas, sistem ventilasi udara, angin laut dan angin darat.

3. Radiasi

Merupakan perpindahan kalor dalam bentuk gelombang elektromagnetik, sehingga radiasi dapat melalui ruang hampa. Permukaan yang hitam dan kusam merupakan penyerap dan pemancar kalor yang baik, sedangkan permukaan putih dan mengkilap merupakan penyerap dan pemancar kalor yang buruk.

              Energi adalah suatu kuantitas yang tercipta dengan sendirinya, yang dapat berubah bentuk atau berpindah dari suatu system ke system lainnya, tetapi jumlah keseluruhannya adalah tetap.

Energi ada bermacam-macam, seperti energi mekanik, listrik, cahaya, kinetik, energi panas dll. Dan perpindahan energi itu dapat terjadi dari energi listrik ke energi mekanik, energi mekanik menjadi energi panas dan lain sebagainya. Dalam percobaan kali ini transfer energi yang kita amati yang terjadi pada pesawat schurholtz adalah transfer energi dari energi mekanik ke energi panas. Perpindahan energi  yang terjadi karena perbedaan temperature disebut dengan perpindahan kalor, dan jika perpindahan tersebut terjadi karena sebuah gaya yang membuat pergeseran posisi benda, perpindahan itu disebut kerja mekanik.

          Usaha mekanik dan panas keduanya merupakan bentuk energi. Bentuk kedua energi ini biasanya dinyatakan dalam satuan Joule (J) untuk energi mekanik dan kalori (kal) untuk energi yang dihasilkan dalam bentuk panas. Sehingga perlu adanya penyetara antara kedua besaran energi tersebut yang disebut Tara mekanik panas, tara mekanik panas merupakan suatu pembanding antara mekanik dan panas. Artinya yaitu suatu pembanding dari satu kalori yang bekerja dalam setiap satu satuan usaha yang ditimbulkan karena peristiwa mekanik.

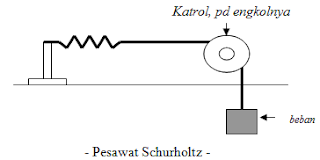
Untuk menentukan tara mekanik panas dari suatu bahan kita dapat menggunakan prisip kerja pesawat Schurholtz. Alat ini berprinsipkan pada gesekan suatu benda terhadap benda lain yang mengakibatkan panas. Energi mekanik dihasilkan dari perputaran engkol yang dihubungkan dengan kalorimeter, yang akan menghasilkan gesekkan dengan pita nilon yang dihubungkan dengan beban. Beban disini berfungsi agar pita nilon, menempel pada kalorimeter yang berputar, sehingga terjadi gesekkan yang cukup menimbulkan panas. Pegas digunakan agar pita nilon dapat bergerak bolak - balik saat engkol diputar dan menghasilkan gesekkan dengan kalorimeter. Ketika pita nilon berputar mengikuti arah putaran kalorimeter, pegas tertarik merenggang, pegas mempunyai gaya pulih yang menyebabkan pita nilon akan tertarik ke arah sebaliknya ke arah putar kalorimeter (kembali pada keseimbangannya), yaitu saat pegas merapat. Gesekkan  pita nilon dengan kalorimeter akan menghasilkan panas pada kalorimeter, dan jika cukup panas akan menimbulkan panas pada kalorimeter, sesuai dengan asas black, bahwa kalor yang diterima kalorimeter sama dengan kalor yang dilepas oleh pita nilon. Bahan tabung kalorimeter disini, memakai alumunium dan tembaga.

Katrol, pd engkolnya diisi termometer,

Pada Pesawat Schurtholtz ini, digunakan beberapa Hukum Fisika yang mendasari prinsip-prinsip kerja dari mesin tersebut yaitu :

Asas Black ini terjadi karena adanya proses pelepasan dan penerimaan kalor antara dua system, dimana untuk kalor yang dilepaskan, pada energi mekanik Jumlahnya akan sama besar kalor yang diterima oleh air.

                                    Kalor yang dilepas = kalor yang diterima

Q_lepas = Q_terima

Jika suatu benda menerima / melepaskan kalor maka suhu benda itu akan naik/turun atau wujud benda berubah. Kalor jenis suatu benda tidak tergantung dari massa benda, tetapi tergantung pada sifat dan jenis benda tersebut. Jika kalor jenis suatu bend kecil maka kenaikan suhu benda tersebut akan cepat bila dipanaskan.

Helmholtz menyatakan bahwa semua bentuk tenaga adalah eqivalen dan bahwa sejumlah yang diberikan dari suatu bentuk tenaga tidak dapat lenyap tanpa sejumlah tenaga yang sama dalam suatu bentuk yang lain. Misalnya pada lilitan pita yang terbuat dari tembaga diberi sebuah beban sehingga diperoleh usaha sebesar :

               W  =    F . s

                     =    m . g . p  .D_kal . n

untuk energi panas yang dilepaskan menjadi :

               Q   =    e . m . g . p  .D_kal . n

kalor yang diterima oleh air :              Q₁ = (m_a . c_a) . DT

kalor yang diterima oleh pita tembaga dan kalori meter :

                                                Q₂ = m_kal . c_{kal .} DT

Menurut Asas Black,kalor yang dilepas sama dengan kalor yang diterima sehingga, system tersebut berada dalam keadaan adiabatic, sehingga dari kondisi seperti itu akan diperoleh harga tara antara energi mekanik dan energi panas, sehingga :              Q    =          Q₁  +  Q₂

Harga Q1 dan Q2 disubtitusikan pada persamaan diatas sehingga, diperoleh :

m . g . p  .D_kal . n      =       (m_ac_a). DT + (m_kal.c_kal). DT

m . g . p  .D_kal . n      =       [(m_ac_a) + (m_kal.c_kal)]. DT

                        

Keterangan :   

e          =  tara mekanik panas ( kal/ joule )

Ma       =  massa air (kg)

Ca        =  panas jenis air (kal/kg.c)

M_kal      =  massa kalori meter tembaga (kg)

c_kal      =  panas jenis tembaga (kal/kg.c)

T      =  perbedaan suhu selama n putaran (c)

n          =  banyaknya putaran

M         =  massa beban ( Kg )

g          =  percepatan gravitasi (m/s)

D_kal      =  diameter kalori tembaga ( m )

Setelah dilakukan percobaannya, saya dapat menganalisa, sebaga berikut :

·         Analisa Data

Pada data ukuran geometri kalorimeter, terdapat 2 jenis bahan kalorimeter yang digunakan yaitu : Alumunium dan Tembaga. Kedua jenis bahan ini akan mempengaruhi besarnya kalor yang dihasilkan dari energi mekanik, karena kedua jenis bahan tersebut memiliki panas jenis yang berbeda.

Pada data kenaikan suhu terhadap banyaknya putaran, terlihat bahwa perubahan suhu pada setiap 20 putaran hingga 500 putaran cenderung menurun. Padahal jika kita lihat dengan teliti rumus yang digunakan diatas, terlihat hubungan antara banyaknya putaran dengan perubahan suhu. Jika jumlah putaran diperbanyak dan kita ingin mendapat nilai tara mekanik e yang tetap maka perubahan suhunya pun harus semakin besar, sehingga didapat nilai e yang tetap. Jadi, menurut teori semakin banyak putaran maka perubahan suhunya pun seharusnya lebih besar.

Pada data yang kita peroleh tidak demikian, hal tersebut dikarenakan perputaran engkol yang tidak konstan sehingga mempengaruhi besarnya gesekan yang akan menimbulkan panas (perubahan suhu) pada kalorimeter. Seharusnya perputaran engkol dilakukan secara konstan/tetap, tetapi perputaran engkol yang kita lakukan terkadang cepat dan terkadang lambat, karena diakhir-akhir putaran tenaga kita sudah terkuras sehingga pada akhir-akhir putaran cenderung lambat memutar engkolnya.

Berdasarkan data, terlihat bahwa pada kalorimeter alumunium besar dan kecil memiliki nilai suhu akhir yag berbeda, pada alumunium kecil suhu akhir lebih besra dibanding alumunium besar, hal ini karena berhubungan dengan massa kalorimeter, berdasarkan rumus diatas terlihat hubungan massa dan ΔT yang berbanding terbalik.

·         Analisa Perhitungan

Untuk menghitung tara mekanik panas, kita gunakan rumus seperti diatas, dalam hal ini praktikum ini kita tidak menggunakan air, sehingga massa air ditiadakan. Sehingga persamaannya adalah : .

Data yang diperlukan dalam menghitung tara mekanik ini adalah massa kalorimeter m_kal, panas jenis kalorimeter c_kal, perubahan suhu ΔT, banyaknya putaran n, massa beban M = 5 kg, tetapan gravitasi g = 9,8 kgm/s², tetapan π=3,14 dan diameter kalorimeter D_kal. Dengan menggunakan rumus diatas dihasilkan nilai KSR yang semuanya cenderung sangar besar yaitu diatas 80%.

Untuk menghitung tara mekanik dengan menggunakan grafik perubahan suhu terhadap putaran, kita menggunakan nilai at dari persamaan grafik at(x)+bt. Kemudian kita hitung nilai e dengan persamaan :

Disini nilai ΔT (perubahan suhu) dan n (jumlah putaran) digantikan dengan nilai at yang didapat dari grafik perubahan suhu terhadap banyaknya putaran, sehingga dengan menggunakan cara ini didapat hasil yang lebih teliti dibandingkan dengan cara sebelumnya, dibuktikan dengan nilai KSR yang lebih kecil dibanding cara sebelumnya yaitu dibawah 33%, bahkan ada yang KSRnya hanya 7%.

            Untuk menghitung kalor yang diserap pita nilon, kita gunakan peramaan :  , dengan    m_kal.c_kal.ΔT = Q

maka untuk menghitung Q, persamaan diatas menjadi : Q = e.n.M.g.π.D_kal

dengan e adalah tara mekanik panas literatur e = 0,24 kal/J

Menurut data, pada jumlah putaran yang sama, kalorimeter dengan diameter lebih besar (kalorimeter 3) memiliki nilai kalor yang lebih tinggi dibanding kalorimeter lain, hal ini sesuai dengan persamaan diatas bahwa kalor yang diserap pita nilon akan sebanding dengan diameter kalorimeter.

          Pada persamaan diatas yang berpengaruh adalah diameter kalorimeter saja, karena tara mekanik yang kita gunakan adalah tara mekanik panas literatur, seandainya yang digunakan adalah tara mekanik panas yang didapat pada perhitungan atau dari grafik, pasti nilai kalor yang dihasilkan pun akan berbeda-beda pada setiap bahan dan tiap lilitan.

·         Analisa Grafik

Grafik yang didapat adalah grafik kenaikan suhu terhadap banyaknya putaran. Dari grafik terlihat hubungan antara suhu terhadap banyaknya putaran dimana semakin banyak putaran maka dihasilkan nilai suhu yang semakin naik. Hal ini karena semakin banyak putaran maka gesekan antara pita nilon dengan kalorimeter akan sering terjadi sehingga menimbulkan suhu yang semakin tinggi. Menurut persamaan  diatas pun terlihat bahwa suhu T akan sebanding dengan jumlah putaran n.

DAFTAR PUSTAKA

Giancoli, C Douglas. 2001 . Fisika Jilid 1. Erlangga : Jakarta

Halliday, Resnick.1988. Fisika Untuk Universitas Jilid 1.Jakarta Pusat : Erlangga.

Nainggolan S. Werlin. 1987. Thermodinamika. Bandung : CV Armico.

Sutrisno dan Tan Ik Gie.1983. Fisika Dasar Listrik Magnet dan Termofisika Listrik. Bandung : ITB

Konstanta Dielektrik

BAB I

PENDAHULUAN

1.1    Latar Belakang

           Dielektrik merupakan suatu bahan yang memiliki daya hantar arus yang sangat kecil atau bahkan tidak ada. Bahan dilektrik dapat berbentuk padat, cair dan gas. Dalam bahan dielektrik memiliki konstanta yang berbeda-beda untuk setiap bahannya. Nilai konstanta listrik dan dielektrik memiliki nilai tetapan yang sebenarnya, namun disini kita akan mencari nilai tersebut melalui eksperimen, untuk menentukan konstantanya yang didapatkan dari hasil pengukuran.

1.2    Identifikasi Masalah

           Bagaimana cara menentukan hubungan antara muatan Q dan tegangan V yang diukur dengan menggunakan pelat kapasitor dan menentukan konstanta listrik ɛ_o dari hubungan tersebut serta dengan memvariasikan jarak antar pelat kapasitor. Bagaimana mengukur muatan pelat kapasitor sebagai invers dari jarak antar pelat pada tegangan konstan, serta menentukan hubungan antara Q dan V yang diukur menggunakan pelat kapasitor dengan media dielektrik antara kedua pelat.

1.3    Tujuan Percobaan

1.      Menentukan hubungan antara Q dan V menggunakan pelat kapasitor.

2.      Menentukan konstanta listrik ɛ_o berdasarkan hubungan V dan Q.

3.      Mengukur muatan pada pelat kapasitor sebagai fungsi invers dari jarak antara pelat pada V konstan.

4.      Menentukan hubungan antara Q dan V dengan mengukur media dielektrik diantara kedua pelat kapasitor

BAB II

TEORI DASAR

A.    Kapasitor

Kapasitor merupakan dua konduktor yang dipisahkan oleh isolator atau bahan dielektrik. Dalam sebuah konduktor, elektron terluar dari sebuah atom sangat mudah untuk terpisah dan berpindah dari satu atom ke atom lainnya bila diletakkan dalam medan listrik. Sedangkan pada suatu dielektrik, elektron lebih mudah meloncat atau diam pada posisi setimbang sehingga mereka tidak bisa terpisah jika diletakkan dalam suatu medan listrik. Jadi, medan listrik tidak memproduksi perpindahan muatan dalam suatu dielektrik. Hal ini yang menyebabkan bahan dielektrik merupakan bahan isolator yang baik. Contoh dari bahan dielektrik adalah parafin, kaca, dan mika.

Dua penghantar berdekatan yang dimaksudkan untuk diberi muatan sama tetapi berlawanan jenis disebut kapasitor atau dapat di artikan sebagai suatu alat yang digunakan untuk menyimpan muatan sementara. Kapasitas suatu kapasitor (C) adalah perbandingan antara besar muatan Q dari salah satu

penghantarnya dengan beda potensial V antara kedua pengahntar itu.Jadi kapasitas kapasitor untuk ruang hampa adalah :

Kegunaan Kapasitor, antara lain :

1.      Untuk menghindari terjadinya loncatan listrik pada rangkaian2 yang mengandung kumparan bila tiba2 diputuskan arusnya.

2.      Rangkaian yang dipakai untuk menghidupkan mesin mobil

3.      Untuk memilih panjang gelombang yang ditangkap oleh pesawat penerima radio.

Bentuk kapasitor, antara lain :

1.      Kapasitor bentuk keping sejajar

2.      Kapasitor bentuk bola sepusat

3.      Kapasitor bentuk silinder

Tetapi kapasitor yang sering digunakan adalah kapasitor keping sejajar. Suatu kapasitor terdiri dari dua keping konduktor sejajar yang terpisah. Ketika konduktor-konduktor dihubungkan pada ujung-ujung suatu sumber tegangan, sumber tegangan tersebut memindahkan muatan dari satu konduktor ke konduktor yang lainnya sampai perbedaan potensial antara ujung-ujung sumber tegangan. Adanya perbedaan potensial antara ujung-ujung sumber tegangan tersebut maka akan terjadi aliran listrik dan alirang listrik ini akan mengakibatkan timbul medan listrik di sekitar kapasitor keping sejajar tersebut.

Pada kapasitor keping sejajar tanpa dielektrik

Karena pada kondisi vakum  jadi

Jika muatan diberikan diantara dua pelat kapasitor,akan terjadi medan listrik E antar pelat yang dinyatakan oleh :

Untuk suatu kapasitor keping sejajar dengan jarak pemisah d, perbedaan potensial antara keping adalah :

Muatan kapasitor Q sebanding dengan tegangan V yang diberikan pada kapasitor, konstanta kesebandingan C dinamakan kapasitansi dari kapasitor ;

Kapasitansi dari suatu kapasitor keping sejajar tanpa dielektrik adalah :

                    dan     

Sehingga besar konstanta listrik

Dimana ;

= konstanta listrik (pAs/Vm)

d = jarak antar kedua keping (m)

A = Luas keping sejajar (m²)

Q = muatan kapasitor (nAs)

Vo = perbedaan potensial tanpa dielektrik (V).

B.     Dielektrik

Dielektrik adalah suatu bahan yang memiliki daya hantar arus yang sangat kecil atau bahkan hampir tidak ada. Bahan dielektrik dapat berwujud padat, cair dan gas.Tidak seperti konduktor, pada bahan dielektrik tidak terdapat elektron-elektron konduksi yang bebas bergerak di seluruh bahan oleh pengaruh medan listrik. Medan listrik tidak akan menghasilkan pergerakan muatan dalam bahan dielektrik. Sifat inilah yang menyebabkan bahan dielektrik itu merupakan isolator yang baik. Dalam bahan dielektrik, semua elektron-elektron terikat dengan kuat pada intinya sehingga terbentuk suatu struktur regangan (lattices) benda padat, atau dalam hal cairan atau gas, bagian-bagian positif dan negatifnya terikat bersama-sama sehingga tiap aliran massa tidak merupakan perpindahan dari muatan. Karena itu, jika suatu dielektrik diberi muatan listrik, muatan ini akan tinggal terlokalisir di daerah di mana muatan tadi ditempatkan.

Konstanta dielektrik merupakan perbandingan energi listrik yang tersimpan pada bahan tersebut jika diberi sebuah potensial, relatif terhadap vakum (ruang hampa).Konstanta dielektrik dilambangkan dengan huruf Yunani ε_r atau kadang-kadang κ, K, atau Dk. Secara matematis konstanta dielektrik suatu bahan didefinisikan sebagai berikut:

                                                      

Penerapan bahan dielektrik ini berdasarkan hukum Gauss. Di mana Gauss menyatakan bahwa jumlah garis gaya atau fluks listrik yang keluar dari suatu permukaan tertutup sebanding dengan jumlah muatan listrik yang dilingkupi oleh permukaan tertutup itu. Secara matematis, pernyataan tersebut dituliskan sebagai :

C.    Kapasitor dengan dielektrik

 Apabila diantara keping sejajar kapasitor ditempatkan dielektrik, maka akan terjadi polarisasi antara dielektrik dengan momen-momen dipol yang searah dengan medan listrik. Ini akan memperlemah medan listrik antara keping-keping suatu kapasitor. Karena dengan hadirnya medan listrik, molekul-molekul dalam dielektrik akan menghasilkan medan listrik tambahan yang arahnya berlawanan dengan medan listrik luar dan ini juga akan mengakibatkan kapasitansi kapasitor menjadi naik.

Pada kapasitor keping sejajar dengan dielektrik

Sehingga besar medan listrik kapasitor keping sejajar apabila telah ditempatkan dielektrik diantara kepingnya adalah :

Kapasitansi dari suatu kapasitor keping sejajar yang berisi dielektrik dengan konstanta k adalah :

Seandainya V sebanding dengan Q, maka kapasitansi tidak bergantung pada muatan maupun tegangan kapasitor tetapi hanya bergantung pada faktor-faktor geometri. Untuk suatu kapasitor keping sejajr,kapasitansi sebanding dengan luas penampang dan berbanding terbalik dengan jarak pemisah.

Sehingga besar konstanta dielektrik dapat dinyatakan dengan persamaan :

Muatan pada kapasitor akan naik secara signifikan oleh dielektrik. Maka diperoleh persamaan sebagai berikut :

                dengan :    atau  

BAB III

PROSEDUR PERCOBAAN

3.1  Alat dan Bahan

1.      Pelat kapasitor, d=260 mm

2.      Pelat plastik

3.      Pelat gelas f current konduktor

4.      Resistor 10 Mohm

5.      Universal measuring amplifier

6.      Power supply, 0-10 kV

7.      Voltmeter, 0.3-300 VDC, 10-300 VAC

8.      Kabel koneksi hijau-kuning, 100 mm

9.      Kabel koneksi merah 500 mm

10.  Kabel koneksi biru 500 mm

11.  Kabel screened, BNC, 750 mm

12.  Adapter, BNC soket 4 mm

13.  Konektor tipe T, BNC

14.  PEK kapasitor 0.22 , 160 volt

3.2     Prosedur Percobaan

A.    Menentukan konstanta listrik

1.    Menentukan luas penampang kapasitor (A), diketahui d=260 mm.

2.    Mengatur tegangan Uc pada 1.5 Kv.

3.    Mengatur jarak pelat kapasitor sekecil mungkin (1 mm), dan mengukur tegangan U dan Q.

4.    Memvariasikan jarak d (d=1.5 ; 2.0 ; 2.5 ; 3.0 ; dan 3.5 mm) dan melakukan pengukuran seperti point 2.

5.    Dengan menggunakan data yang diperoleh, menghitung  dengan menggunakan persamaan 4.

Catatan : selama melakukan pengukuran tidak berada di dekat kapasitor.

B.     Kebergantungan muatan induksi pada tegangan

1.   Mengatur jarak antar pelat d = 2 mm.

2.   Mengukur tegangan U (Volt) dengan pemberian Uc sebesar 0.5 ; 1.0 ; 1.5 ; 2.0 ; 2.5 ; 3.0 dan 3.5 Kv.

3.   Menentukan nilai Q.

4.   Dengan menggunakan data yang diperoleh, menghitung  dengan menggunakan persamaan 4.

C.    Menentukan konstanta dielektrik pelat plastik

1.   Memasang pelat plastik (d=9.8 mm) diantara pelat kapasitor.

2.   Mengukur tegangan U (Volt) dengan memberikan tegangan Uc sebesar 0.5 ; 1.0 ; 1.5 ; 2.0 ; 2.5 ; 3.0 ; 3.5 dan 4.0 Kv.

3.   Menentukan harga Q (nAs) dan

4.   Melepaskan pelat plastik.

5.   Pada jarak yang sama antar pelat dengan tebal pelat plastik (d=9.8 mm), mengukur tegangan Uvac(Volt) dengan memberikan tegangan Uc sebesar 0.5 ; 1.0 ; 1.5 ; 2.0 ; 2.5 ; 3.0 ; 3.5 dan 4.0 Kv.

6.   Menentukan harga Qvac (nAs) dan membandingkan harga Q dengan Qvac

D.    Menentukan konstanta dielektrik pelat gelas

1.    Memasang pelat kaca antara pelat kapasitor dan mengukur ketebalan pelat kaca.

2.    Melakukan pengukuran dan perhitungan seperti pada langkah C.